InterNet
Control and
Inference
Tools at the
Edge
Network traffic modeling
| Real WAN Traffic |
MWM (multiplicative) model |
fGn (additive) model |
![[WAN traffic at 6 msec]](figures/bmw_lev_bellaug1.jpg) |
![[Multifractal model at 6 msec]](figures/bmw_lev1.jpg) |
![[Gaussian model at 6 msec]](figures/wig_lev1.jpg) |
![[WAN traffic at 24 msec]](figures/bmw_lev_bellaug3.jpg) |
![[Multifractal model at 24 msec]](figures/bmw_lev3.jpg) |
![[Gaussian model at 24 msec]](figures/wig_lev3.jpg) |
Left: Bytes-per-time arrival process at different aggregation
levels of
wide-area traffic observed at the Lawrence Berkeley Laboratory.
Middle and Right: One realization of a multifractal wavelet model (MWM)
respectively a Gaussian wavelet model (fGn)
which both match the correlation structure of the data exactly.
However, the MWM is not only visually a better fit as is explained below.
Timeresolution: Top at 6 msec, Bottom at 24 msec.
The need for multiscale modeling
It has for long been realized that efficient and accurate modeling
of various real world phenomena needs to incorporate the fact that observations
made on different scales each carry essential information. In most simple
terms, representing data on large scales by its mean is often useful (such
as as `average income' or an average number of clients per day) but can
be inappropriate (eg. in the context of buffering or waiting queues).
Classical models of time series such as Poisson and Markov processes
rely heavily on the assumption of independence, or at least weak dependence.
So do classical limit theorems such as the Law of Large Numbers which states
that at large scales a Poisson process can safely be approximated by its
mean arrival rate. However, in real world situations one is confronted
with data traces which are `spiky' and `bursty' even at large scales. Such
a behavior is caused by strong dependence in the data: large values
tend to come in clusters, and clusters of clusters, etc. This is as true
for the classical data of the River Nile as for modern high speed communication
networks and has obvious and far-reaching consequences ranging from reservoir
and buffer design to bandwidth allocation to name but a few.
Fractal Models
Aimed at modeling at multiple scales, fractional Brownian motion (fBm)
is able to capture and incorporate long range dependence (LRD) at least
in terms of second order correlations. In this attractive fractal
model, LRD is directly coupled to a rescaling property which makes fBm
look `statistically identical' on all scales. Being a Gaussian process
fBm is a natural candidate for an approximation of LRD-traces, at least
at large scales due to the Central Limit Theorem (CLT) which states roughly
that sums of random variables (ie. highly aggregated or large-scale data)
tend the Normal distribution.
Multifractals
Like fractal models, multifractals are inherently multiscale objects
with strong rescaling properties, but with the essential difference of
being built on multiplicative schemes. Naturally, they are highly
non-Gaussian and are ruled by different limiting laws than the additive
CLT, more precisely by martingale theorems. Moreover, multifractals exhibit
exactly that `spiky' and `bursty' appearance which we encounter now in
many real world situations such as Internet traffic loads, web file requests,
geo-physical data, images and many others.
Multifractal spectrum
The LRD built into fractal models helps address strong correlations
and high variability, especially on large scales or aggregation levels.
Bursts, however, are much better understood in terms of a local
scaling analysis which is designed to capture not only an overall behavior
but rather also rare events such as bursts. This is exactly what
the multifractal spectrum f(a) provides in terms of a large deviation
principle: given the strength of a burst measured with the exponent
a
the value f(a) indicates how frequently this strength a will
be encountered. The larger f(a) the more often one will see
a.
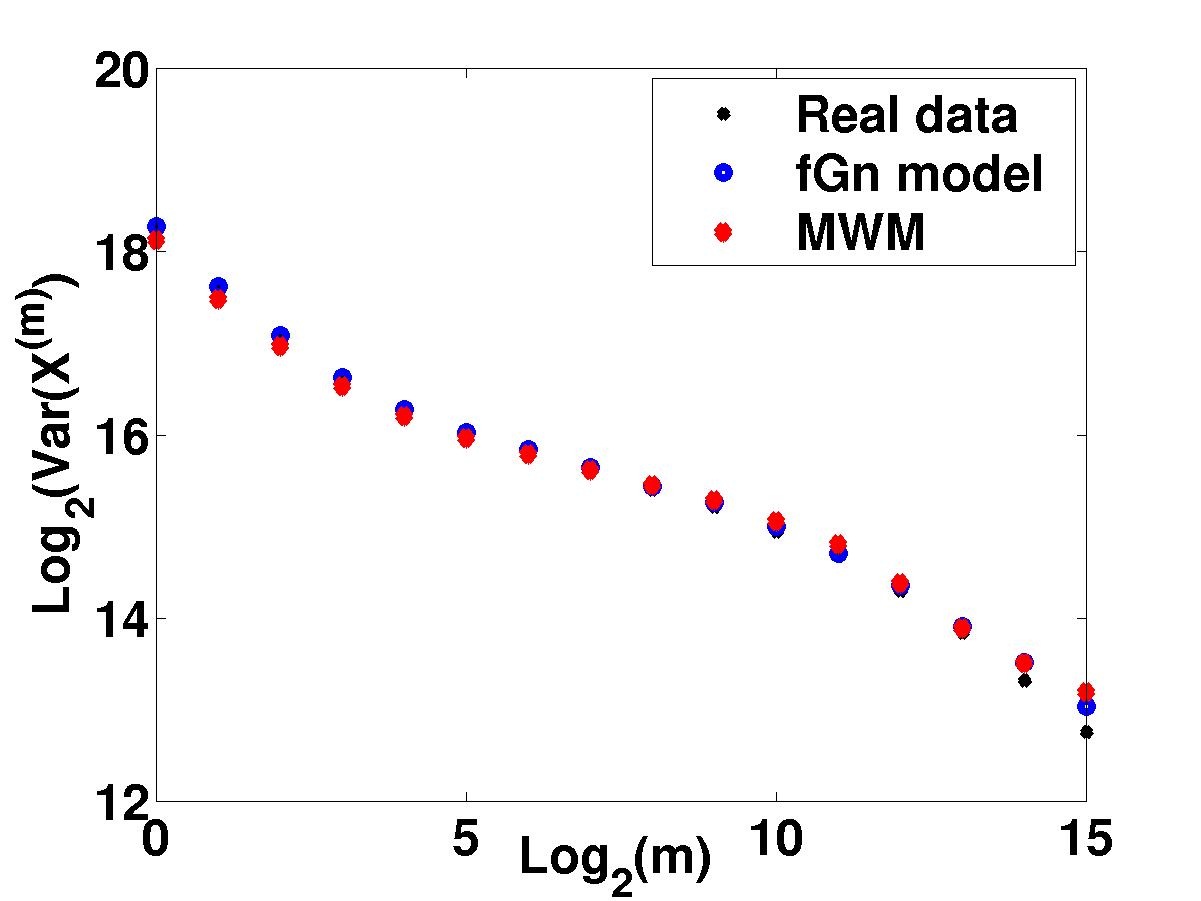
| Variance time plots indicate that both the MWM
and the fGn exactly match of the second-order correlation structure of
the Bellcore data.
|
|
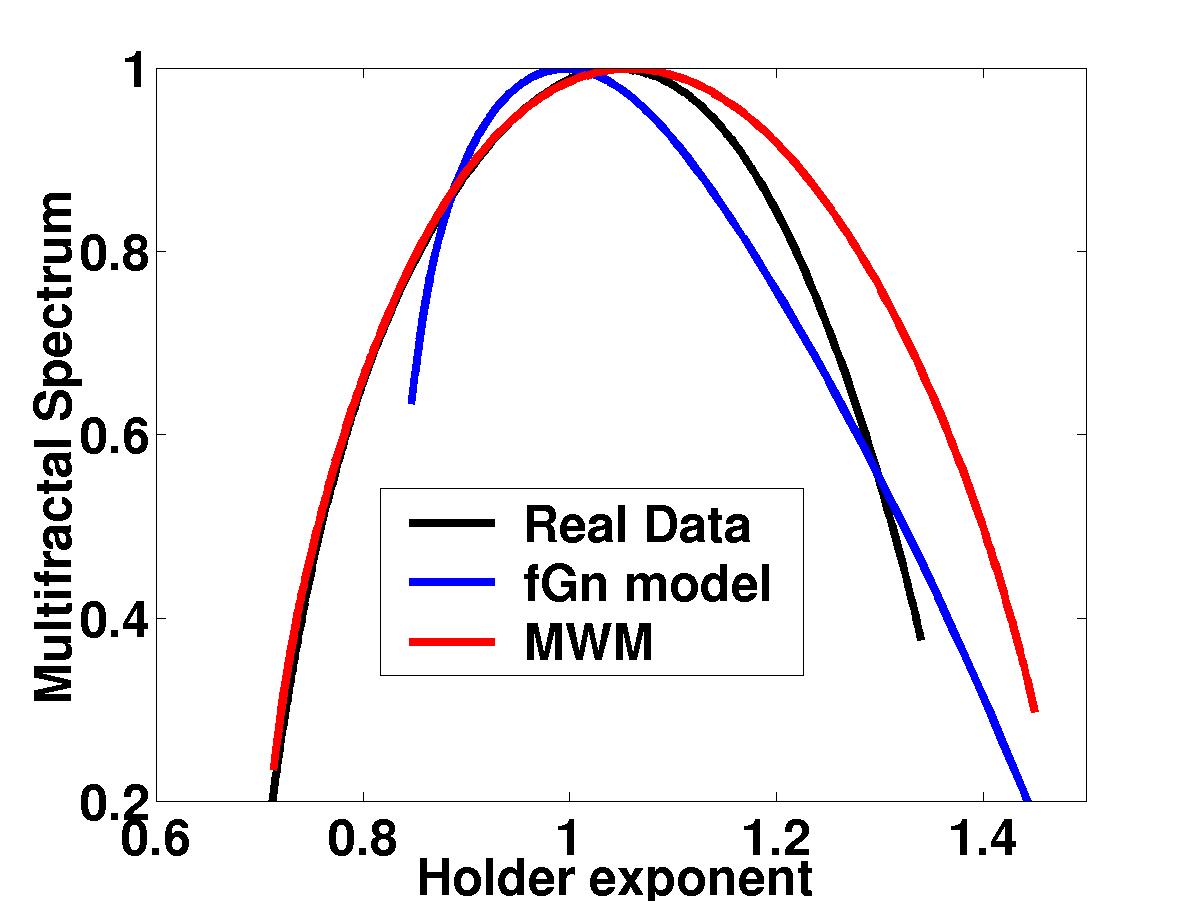
| Multifractal spectrum measures the
"burstiness" of a time trace through the scaling of its higher-order
moments. Note the close match between the spectra of the MWM and
Bellcore data, particularly in the left half of the curves. This is a
quantitative explanation for the close visual match we see above. In
contrast, the fGn match is poor. The MWM comes with its own toolbox
of powerful multifractal analysis techniques for characterizing
traffic burstiness and long-range-dependence.
|
|
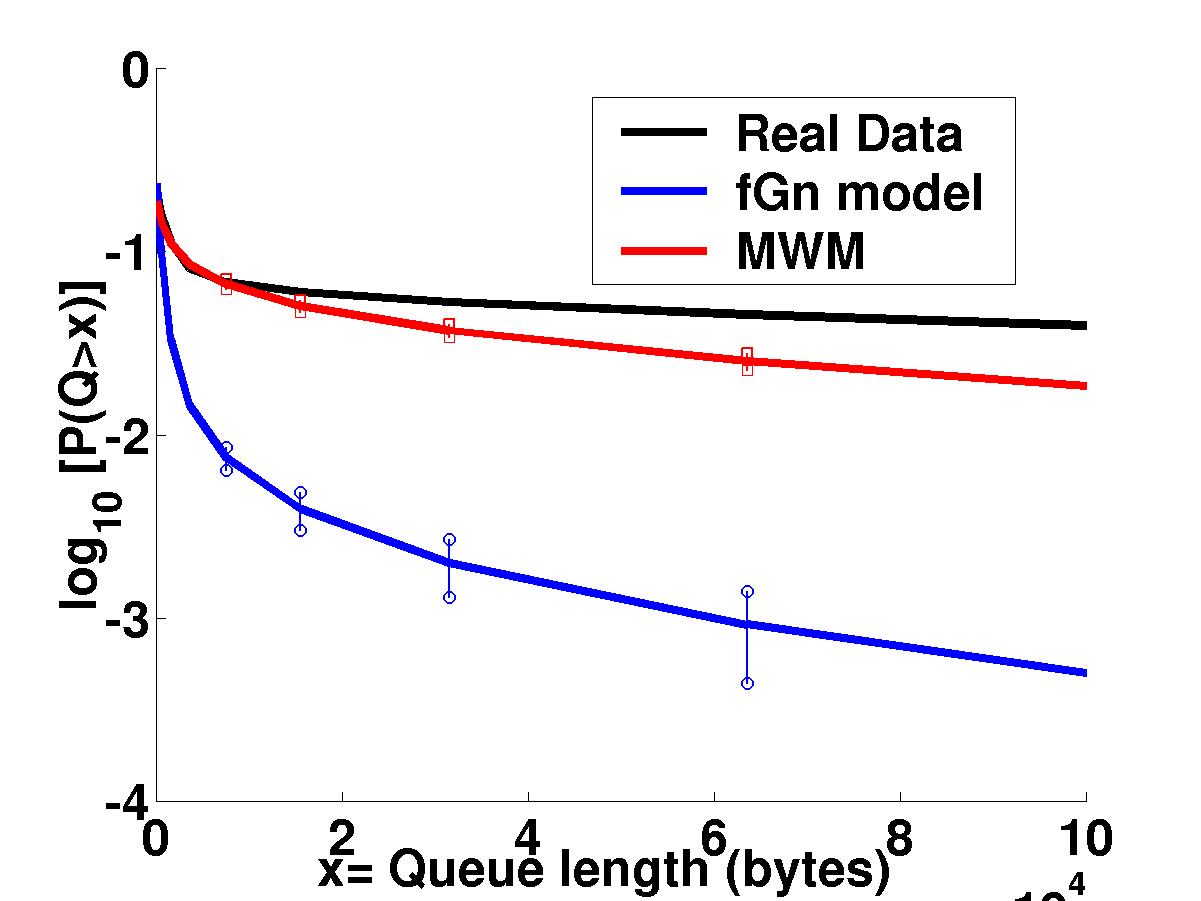
| More important than either the visual
or multifractal spectrum match is the fact that the MWM synthesized
data has nearly the same queuing behavior as the real data,
again in contrast to the fGn model. Here we plot the queue overflow
probability as a function of queue size. We have developed an
analytical formula for the MWM curve, which will be vital for online
traffic characterization and performance prediction.
|
|
Publications
Books on Multifractals:
![[WAN traffic at 6 msec]](figures/bmw_lev_bellaug1.jpg)
![[Multifractal model at 6 msec]](figures/bmw_lev1.jpg)
![[Gaussian model at 6 msec]](figures/wig_lev1.jpg)
![[WAN traffic at 24 msec]](figures/bmw_lev_bellaug3.jpg)
![[Multifractal model at 24 msec]](figures/bmw_lev3.jpg)
![[Gaussian model at 24 msec]](figures/wig_lev3.jpg)


