References:

Campbell, J. (1996) Introduction to Remote Sensing. The Guilford Press.

Clark. R. N. (1999) Spectroscopy of Rocks and Minerals, and Principles of Spectroscopy, In Manual of Remote sensing. John Wiley and Sons, Inc A. Rencz, Editor New York 1999. Manuscript available at http://speclab.cr.usgs.gov

Howell, E. S., Merényi, E., L. A. Lebofsky (1994) Using Neural Networks to Classify Asteroid Spectra, JGR Planets, 99 No. E5, pp 10,847-10,865.

Merényi, E., E.S. Howell, L.A. Lebofsky, A.S. Rivkin (1997) Prediction of Water In Asteroids from Spectral Data Shortward of 3 Microns, ICARUS, 129, pp 421-439.

Merényi, E., Farrand, W.H., Minor, T.B., Taranik, J.V. (1999b) Efficient Geologic Mapping From Hyperspectral Images With Artificial Neural Networks Classification:a Comparison To Conventional Tools. In preparation for submission to IEEE Trans. on Geoscience and Rem. Sens.

Merényi, E. et al. (1999c) Data Mining in Large Spectral Images Using Self-Organizing Maps. In preparation for submission to IEEE Trans. on Neural Networks.

Some slides are poorly resolved here. For an MS Word document version, email me at erzsebet@pirlmail.lpl.arizona.edu.

Slide 1

The problem:

Remote spectral imaging of planetary surfaces is a leading technique for resource mapping. Hyperspectral imaging can identify material because it resolves the discriminating narrow spectral features (see slides 2 and 3). Examples of spectral/hyperspectral imagers are: Earth: AVIRIS, Hyperion (to be launchen on EO-1, Dec 1999); Mars: Pathfinder IMP, Global Surveyor TES; outer planets: Galileo NIMS, Cassini VIMS.

Clustering and classification of these data has become an issuse with increasing spectral and spatial resolution. Spectral images are huge, and complex. Exploitation poses a problem both in terms of speed (on-board, real-time knowledge extraction) and interpretation Conventional tools often perform poorly for high spectral dimension.

Why ANNs, and why Self-Organizing Maps (SOMs)?

We need tools that match up to the intricacy of the data, to avoid the need to degrade data in order to use an old tool. ANNs as massively parallel algorithms, provide speed (when implemented in hardware); they also surpass conventional classifiers (when properly used). SOMs, specifically, are better for large, real-life tasks than more conventional ANN paradigms. In this AISRP project we engineer & integrate SOMs and SOM -hybrid ANNs and related knowledge extraction modules, to achieve working solutions for the above problems. The long term vision is hardware implementation for real-time, on-board "precision mining" of large spectral data volumes.

Slide 2

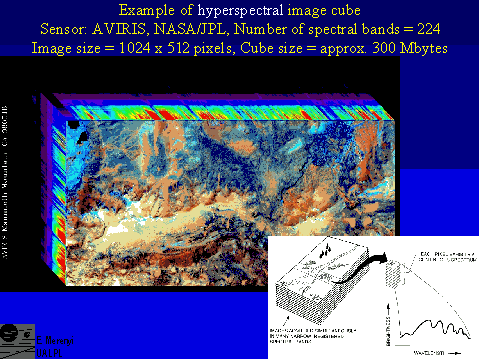
An example of hyperspectral image, acquired by AVIRIS over Mammoth Mountains, Ca. Containing 1024 x 512 pixels in 224 spectral bands, this image is approximately 300 Mbytes.

Insert is from Campbell, 1996.

Slide 3

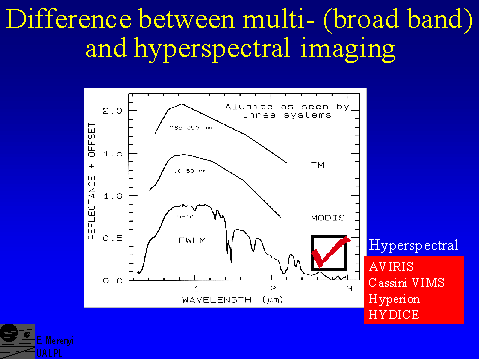
Spectral signatures of materials are resolved well enough by hyperspectral sensors to recognize narrow absorbtion bands measured in the laboratory. Based on specific bands and band shapes, the mineralogy can be identified. Broad band multi-spectral sensors do not provide that capability. But hyperspectral data are huge: an AVIRIS (224 bands) image is more than 30 times larger than a Landsat TM image of the same spatial size.

Spectra are from Clark, 1999.

Slide 4

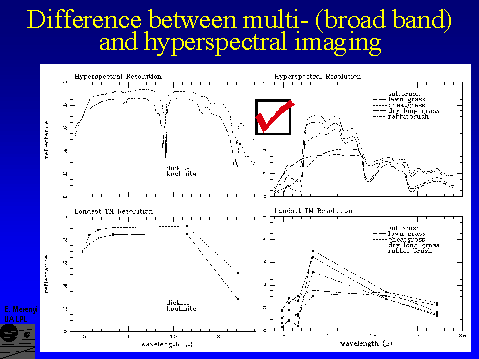
Examples of spectral signatures of minerals and plants, as resolved by AVIRIS and Landsat TM.

Slide 5

Slide 6

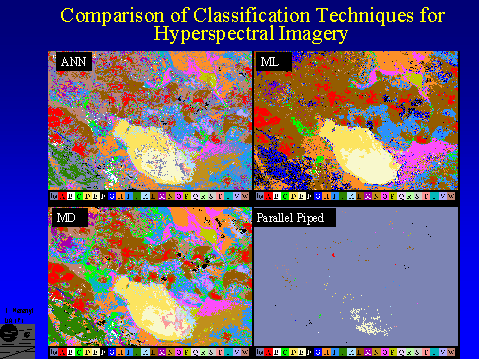
Comparison of supervised classifications by an SOM-hybrid ANN and three conventional methods. (Images from Merényi et al, 1999b.) The source data is a 194-band, 512 x 614 pixel AVIRIS image of a 10 x 12 square km area over the Lunar Crater Volcanic Field, Nevada. The image comprises 140 Mb of data. It contains, among other materials, volcanic cinder cones (class A, red) and weathered derivatives thereof such as ferric oxide rich soils (L, W), basalt flows of various ages (black and blue classes, F, G, I), a dry lake divided into two halves of sandy (D, dark yellow) and clayey composition (E, light yellow); a small rhyolitic outcrop at the bottom (B, white); and some vegetation at the lower left corner (J, dark green). A long linear feature (G, dark blue) bordering the vegetated area is a scarp, along which a certain type of basalt is exposed. 23 geologic cover types were defined and used for training. See Merényi, 1998, for spectral signatures of these classes and better resolved image.

Upper left: ANN classification map. No dimensionality reduction was done before classification. 194 bands remained from the 224 oiginals after eliminating useless information (saturated atmospheric, overly noisy, and overlapping bands). The spectral detail in the data allows distinction of many relevant classes in the scene, including volcanic cinders (A) and weathered derivatives (L, W), young and old basalts (F, G, I), and dry playa and outwash materials with various clay and moisture contents (E, D, Q -- T; and N -- P).

Upper right: Classification of the same spectral image by Maximum Likelihood technique. It is apparent at first glance that many classes have been lost due to inadequate discrimination. For ML, the number of bands had to be reduced to 32, because for some classes (e.g., B, Q, R, S, T) even 30 training samples were difficult to confidently identify. Consequently this comparison is "unfair" for ML, however, it illustrates a severe limitation of this classifier in real-life situations of remote sensing.

Lower right: Parallel Piped classification loses most of the classes, due to rigid rule based class definition, which works poorly for noisy spectra and classes with variable ``tightness".

Lower left: Minimum Distance classification comes closest to the ANN results. It also looks more pleasing because this MD classifier assigns every pixel to a class while the ANN leaves some pixels unclassified. Closer examination, however, reveals more misclassifications by MD than by ANN. PP and MD also used all 194 bands.

The ANN classifier is an SOM-hybrid (described in Merémyi et al., 1997, Howell et al., 1994): the SOM component forms clusters in an unsupervised regime before the actual supervised classification begins. This helps prevent learning inconsistent information; enables better generalization from small number of training samples (a REAL problem in remote sensing!), which results in more accurate classification. Selection of correct training samples is also important. We developed a related integrated interactive tool under this AISRP project (EXPLORE, different from tools available in popular packages) to aid in that. The advantage of ANN over the other classifiers increases with increasing spectral dimensionality. (ML can do good job for, e.g., Landsat TM = 6 bands, since 6+1 = 7 training samples per class - required for ML to avoid singular covariance matrix - are not difficult to find. Identifying >200 training samples per class for the above 23 classes, however, can be prohibitively labor intensive, or impossible for very small classes.)

We do not know of other ANN research that tackled hyperspectral images with full spectral resolution. Typical approach is to reduce dimensionality (accept loss of information) in order to use a Back Propagation ANN, which is difficult to train, and scales up poorly for large tasks.

Slide 7

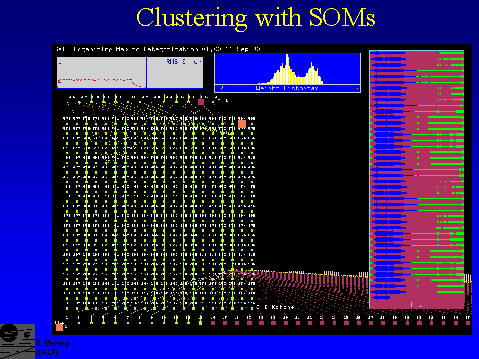
Screen display of SOM-hybrid ANN. The hidden layer is a 2-D Kohonen Self-Organizing Map.This display is from NeuralWare’s NeuralWork Plus II, whith which we construct ANN paradigms in a graphical development environment. After development and testing, the ANN is deployed into an independent C module (written by us), which we use for accessing any part of the network , and for creating specialized interfacing and visualization functionalities for spectral image analyses. The slides below are from screen displays of modules developed under this AISRP project.

Slide 8

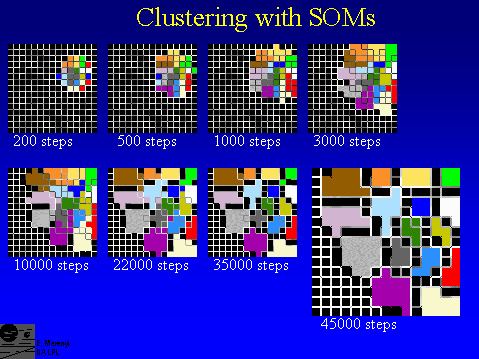
A "toy" example of cluster formation by a SOM. The source data set is a synthetic, 128 x 128 pixel, 6-band spectral image that contains 16 different spectral types.

The spectral types are known to us, but not known to the SOM. During unsupervised training, the SOM learns to distinguish them and sorts them into separate clusters. The process is illustrated here. Data points of the same spectral type are colored the same, to see if the SOM clusters the data correctly. The white fences delineating the final clusters develop during the learning process. They are representing the difference of the weights of neighboring SOM neurons. The larger the difference, the more dissimilar the data that are mapped to the corresponding adjacent neurons. In this case, the SOM contains 15 x 15 neurons. Note that the fences completely disappeard within the final clusters, indicating strong similarity among data points  within clusters. Image material from Merényi et al, 1999c.

Slide 9

The same clustering as in side 8, shown without the colors (which are only known to us but not to the SOM).The inset has been scaled up in intensity so that all neurons onto which data points were mapped are visible. The intensity of the red color is proportional to the number of pixels (6-D spectra) mapped onto the corresponding neuron. On the left, the same mapping is shown unenhanced, indicating that the majority of the data points in each cluster is mapped onto one neuron. This is justified in the case of this synthetic image, since data were generated by applying small random noise to each of the sixteen prefabricated spectral types. Image material from Merényi et al, 1999c.

Slide 10

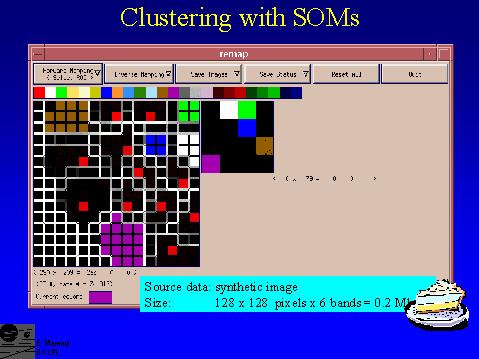
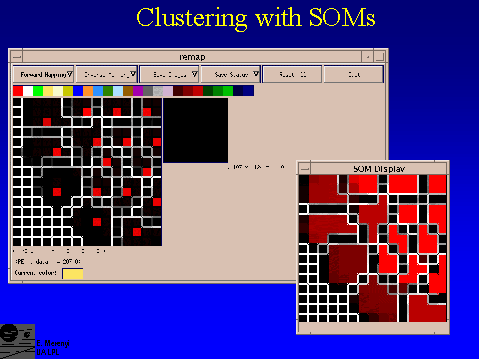
Screen display from the REMAP tool. Clusters detected by the SOM (left) are circled by the mouse and, by one click the cluster will be colored to a color preselected from the  (user defined) color wedge. At the same time, the corresponding pixel locations in the spatial image (right) will be colored the same.

This is an example of a partial re-mapping of the clusters detected in the small, 128 x 128 pixel,  6-band synthetic image in slides 8 and 9. Note, for example, that the brown cluster was not fully covered (one SOM neuron , which does have data points mapped onto it (slide 9), was left out). The corresponding spatial area in the image shows unmapped (black) speckles. Seeing and delineating the clusters for this "toy" case is a piece of cake.

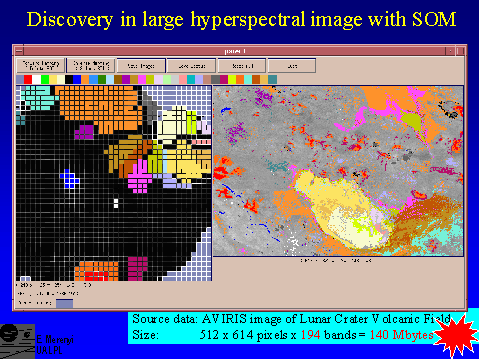
Slide 11

Clusters identified from a knowledge representation display of a 40 x 40 Self-Organizing Map (left), and the corresponding spatial regions (right). The input data set is the same 194-band, 140 Mbyte AVIRIS spectral image as in slide 6. The full spectral resolution was utilized in producing these 32 clusters, in an unsupervised procedure. Screen display is from the graphical user interface of the REMAP tool. Image material from Merényi et al, 1999c.

This clustering is a striking match to the supervised ANN class map in slide 6, upper left. It means that the SOM detected all the classes that were known to us as meaningful geological units. In addition, the SOM detected more, spatially coherent, clusters than the number of classes in slilde 6. The most obvious discovery of a spatially small area of ``interesting" material was the dark blue cluster, which delineates the long scarp at the lower left corner of the image (indicated by the number 1). It corresponds to class G  in slide 6. The maroon cluster at the bottom (indicate by the number 2), filled in several areas, adjacent to volcanic cinder cones, that were left unclassified in slide 6. The areas that were mapped as class A (red) in slide 6, are separated here into two clusters (red and dark orange), delineating spatially coherent subareas: the centers and flanks of the cinder cones. The embedded sequence of red, dark orange, brown, maroon and mauve clusters (upward and outward from bottom center of the SOM) outline materials in the spatial image that change from hematite rich cinders to increasingly weathered derivatives. Another good example for the detection of a spatially small cluster of material that is distinguished by a subtle spectral difference from its surroundings, is the lightest blue cluster (indicated by the number 3). It outlines a thin rim of the dry lake, and a few patches where basalt cobbles are scattered. The spectral difference from the signature of the dry lake is subtle because the playa surface contributes heavily to each pixel due to low aerial coverage by the cobble stones.

Slide 12

Partially interpreted version of the map in slide 11.

Slide 13

Possible visualizations of SOM clustering. The input data set is the 194-band AVIRIS image of Lunar Crater Volcanic Field, used in slides 6 and 11. Underlying the interpreted cluster map in slide 11, is one of several possible representations of the cluster information, extracted from the SOM, such as shown here. Image material from Merényi et al, 1999c.

Center: ``Walls" calculated from the weights of SOM neurons, representing the degree of separation between clusters by the intensity of white grid lines. Neurons where no data points were mapped are shown in grey background color.

Right: In addition to the walls on the left, information is provided on the number of data points (image pixels) that were mapped onto each of the SOM neurons. This is visualized in the form of a monochrome (red) density map underlying the walls. The intensity of the red color of each cell is proportional to the number of data points mapped to the that cell.

Left: The density map without the walls.

The colored areas in slide 11 are produced in an interactive REMAP session: The user starts with a cluster representation (such as these) on the left of the REMAP workspace, and a blank spatial image on the right, outlines the detected clusters with a screen pointer and colors that area to a color selected from a user-defined color wedge. The corresponding pixels in the spatial image will be highlighted in the same color automatically. [Instead of a blank image, any representation of the spatial area can be used (such as a grey scale band from the spectral image), to provide a quick visual check for the spatial context of the remapped clusters.]

We are working on various issues related to the effective interpretation of maps like these. Ideally, the combined density and fence map provides the full knowledge of the SOM. But many details need to be addressed. For example, by overlaying the two maps the fences around the brightest group became almost invisible due to contrast and color relations that trick the human eye.We have built in various on-the-fly capabilities to change such visualization parameters during a REMAP session. This is important also because optimal display for the human eye may vary from one part of the SOM to another.

We gained insight with these tools, which helps get closer to full automation of the interpretation of the SOM. (Nobody has done it yet. The most experienced group, Kohonen’s at Helsinki U of Technology, which pioneered the SOM, as well as the large scale applications of SOMs, uses these visualizations (often the density map alone) to click/browse in large text bodies (library catalogs), which are organized by the SOM according to similar subjects. Their applications do not demand actual delineation of clusters, like ours does.)

Slide 14

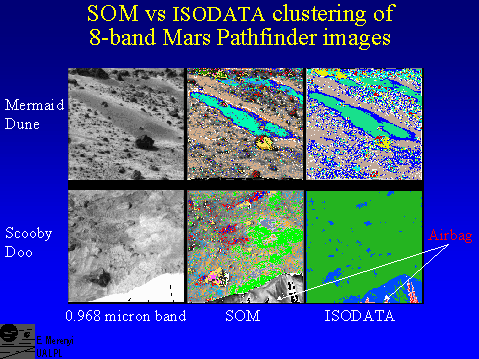
Even for lower dimensionality, such as this IMP, Mars Pathfinder image, there are advantages in using SOMs. ISODATA and SOM clustering are shown for two IMP spectral images. The left panels are 0.968 micron band images, to show scene details.The upper row is the ``Mermaid Dune", for which SOM (middle)and ISODATA (right) detected similar clusters. Note, however, that the detail in the SOM is higher. The lower row is an ``unusual" case, and illustrates how robust algorithms can be useful for such situations. The area is that near the rock ``Scooby Doo", very close to the lander unit. Visible at the bottom is the airbag sticking out from underneath the lander. (In the 0.968 micron grey scale image the airbag is extremely bright because the scene had to be brightened in order to see the details of rocks and soils. The SOM clustered imge shows the original appearance of the airbag.) This material (a ``noise" for us) is drastically different from the surrounding geologic surfaces (our interest) and there are many shade variations within it. ISODATA assigned most of the 64 allotted clusters to the airbag. Only after requesting more than 64 clusters, started meaningful distinctions appear within the area containing rocks and soil. The SOM clustering and visualization captured the important distinctions at once.

Slide 15

Partially interpreted SOM of the 8-band IMP image Scooby Doo.

The pixels coming from the airbag were strongly separated and far away from all geologic materials. The same is true for some "garbage" at image edge.The empty black patch toward the lower left contained one neuron onto which all pixels from some weird noise in several lines at the bottom of the image were mapped. (Different from the "garbage" indicated above.) That cell was so bright that it set off the scaling for all others, so I simply deleted it for display purposes. But it again demonstrates how smart the SOM is.

Notes for future direction and work:

One of the crucial concerns in using SOMs is the correctness /reliability of the topological mapping from higher-D space to 2-D. With small data sets such as in our asteroid taxonomy studies (Howell et al., 1994, Merényi et al., 1997) we could examine the SOM in a semi-manual manner, and observe occasional ``entangling" of clusters: some data points became ``stuck" in one part of the SOM while they clearly belonged to some cluster that formed in another part of the SOM. Reasons for this phenomenon can be, for example, that the intrinsic dimensionality of the input space is too high for correct mapping onto a 2-D SOM; or that the SOM lattice is too small causing a boundary effect (as shown in Merényi et al. 1997). Convergence of the weights can be monitored easily; however, convergence does not equate to correctness of the clustering. While aware of the possibility of erroneous clustering, with large data sets it is very difficult, if not impossible, to detect these conditions unless many hours are spent on checking every SOM map. With small data sets that require short processing time, incorrect clustering can usually be remedied by a new run with a different random initial state, wich could produce a problem-free clustering. For large data sets, even if we notice the incorrect mapping, repeated runs are expensive. To cluster the AVIRIS image shown in slide 11., for example, takes about 24 hours on the PI's current Sun Ultra 1. (It is no consolation that ISODATA takes 2-3 days for the same image.) Leaving the long run time aside (because the same process will take mere seconds if implemented in parallel hardware), the effort needed to detect the ill conditions is still tremendous, certainly impractical.

Theoretical research has addressed this problem. Recently some results were obtained that offer practical solution for our purposes (Villmann et al., 1997, Bauer et al., 1997). This work is based on findings by Martinetz and Schulten (1994), and carry it further in that it provides a formula., incorporation of which willalert immediately for entanglement of clusters. The work of Villman et al. also provides an algorithm forextending the SOM clustering by automatically growing the SOM lattice to relieve topology violation (Bauer and Villman, 1997; Villmann and Bauer, 1998). We plan to implement these algorithms into our software, in a close collaboration with Dr. Villmann, who will provide code.

These issues are also related to intrinsic dimensionality determination and thus results may bear on fast data compression of spectral images (Bruske and Sommer, 1998; Bruske and Merényi, 1999; Amerijckx et  al., 1998).

References for "Notes":

Amerijckx, C., M. Verleysen, P. Thissen, and J-D. Legat (1998) Image Compression by Self-Organized Kohonen Map. IEEE Trans. on Neural Networks, 9(3), 503-507.

Bauer, H.U., Herrmann, M., Villmann, Th., (1997) Topology Preservation in Neural Maps of Real World Data. Proc. 5th European Symposium on Artificial Neural Networks, ESANN'97, Bruges, Belgium, April 22--24, 1997, 205-210.

 Bauer, H.U., and Villmann, Th ({1997) Growing a Hypercubical Output Space in a Self-Organizing Feature Ma. IEEE Trans. on Neural Networks, 8(2), 218-226.

Bruske, J., and Sommer, G. (1998) Intrinsic Dimensionality Estimation with Optimally Topology Preserving Maps. IEEE PAMI, 20(5), 572-575.

Bruske, J., Merényi, E. (1999) Estimating the Intrinsic Dimensionality of Hyperspectral Images. Proc. European Symposium on Artificial Neural Networks, ESANN'99, Bruges, Belgium, 21-23 April, 1999, 105-110.

Villmann, Th., Herrmann, R.Der, and Martinetz, Th. (1997) Topology Preservation in Self-Organizing Feature Maps: Exact Definition and Measurement. IEEE Trans. on Neural Networks, 8(2), 256-266.

Villmann, Th. and Bauer, H.-U (1998) Applications of the growing self-organizing map, Neurocomputin, 21, 91-100.