ELEC 242 Lab
Background
DC Motor: Torque vs. Speed
Consider a DC motor with armature resistance
 , torque constant
, torque constant  , and back emf constant
, and back emf constant  being driven by a voltage source
being driven by a voltage source  .
.
![\includegraphics[scale=0.650000]{ckt9.3.ps}](img247.png)
 represents the combined moment of inertia of the motor
armature and the load.
Then we have
represents the combined moment of inertia of the motor
armature and the load.
Then we have
 .
From the coupling equations we have
.
From the coupling equations we have
 and
and  .
Combining these along with Ohm's law, we get:
.
Combining these along with Ohm's law, we get:
 where
where
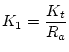 and
and
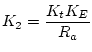
System Transfer Function
In terms of the angle of rotation of the drum  , the equation
describing the system is
, the equation
describing the system is
 where
where
-
-
 is the summing amplifier gain
is the summing amplifier gain
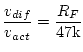
-
-
 is the equivalent moment of inertia seen at the shaft, including the
effects of the load mass.
is the equivalent moment of inertia seen at the shaft, including the
effects of the load mass.
-
-
 is the gain of the potentiometer (
is the gain of the potentiometer (
 ).
).
-
-
 is the equivalent torque caused by the weight of the load.
is the equivalent torque caused by the weight of the load.
-
-
 is the desired angle of the shaft.
is the desired angle of the shaft.
Making the substitutions
 and
and
 we get
we get
 Using superposition we define
Using superposition we define
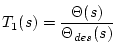 with
with  and
and
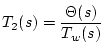 with
with
 .
Then
.
Then
 .
Evaluating
.
Evaluating  and
and  we have
we have
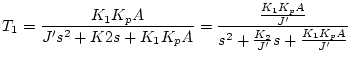 and
and

Some observations
-
In the steady state,
 ,
i.e. there is no steady state gain error regardless of A.
If
,
i.e. there is no steady state gain error regardless of A.
If  there will be a constant offset, but
there will be a constant offset, but
 .
.
-
 falls off as
falls off as  ,
i.e. disturbance rejection increases with increasing gain.
,
i.e. disturbance rejection increases with increasing gain.
-
System dynamics depend on
 .
The characteristic equation is
.
The characteristic equation is
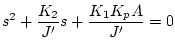 .
This is our familiar second order system with
.
This is our familiar second order system with
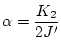 and
and
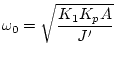 .
So as
.
So as  increases, the system eventually becomes underdamped
and will oscillate.
increases, the system eventually becomes underdamped
and will oscillate.
![]() , torque constant
, torque constant ![]() , and back emf constant
, and back emf constant ![]() being driven by a voltage source
being driven by a voltage source ![]() .
.
![\includegraphics[scale=0.650000]{ckt9.3.ps}](img247.png)

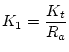 and
and
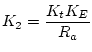
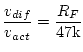
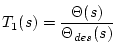 with
with 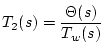 with
with
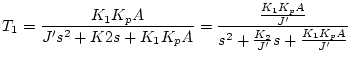

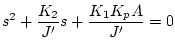 .
This is our familiar second order system with
.
This is our familiar second order system with
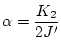 and
and
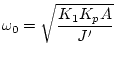 .
So as
.
So as