PLA Decoder

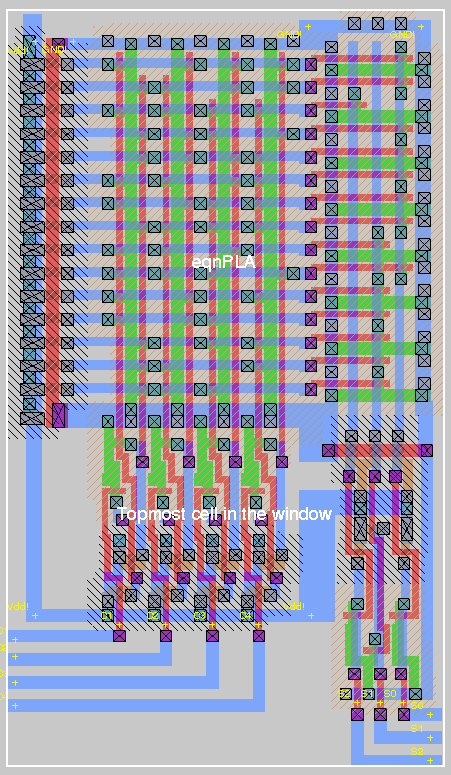
These equations will be entered into a tool to build a PLA that will perform the logic:

Most significant bit:
S2 = C1*C2*C3*C4

Middle significant bit:
S1 = C1*C2*C3' + C1*C3'*C4 + C1*C2'*C4 + C1*C2'*C3 + C1*C3*C4' + C2*C3*C4' + C1'*C2*C3 + C1'*C3*C4 + C1'*C2*C4 + C2*C3'*C4

Least significant bit:
S3 = C1*C2'*C3'*C4' + C1'*C2*C3'*C4' + C1*C2*C3'*C4 + C1'*C2'*C3'*C4 + C1*C2'*C3*C4 + C1'*C2*C3*C4 + C1*C2*C3*C4' + C1'*C2'*C3*C4'

The inputs are the results of a 4 peg comparison between the key and the guess, which returns C1, C2, C3, and C4. The outputs, S2, S1, and S0, describe the sum of the number of inputs that are high. Therefore S2-S0 tell the number of peg matches that occured.

Input to eqntott for PLA Decoder

INORDER=
C1
C2
C3
C4;

OUTORDER=
S2
S1
S0;

S2=
(C1&C2&C3&C4);
S1=

(C1&C2&!C3)| (C1&!C3&C4)| (C1&!C2&C4)| (C1&!C2&C3)| (C1&C3&!C4)|
(C2&C3&!C4)| (!C1&C2&C3)| (!C1&C3&C4)| (!C1&C2&C4)| (C2&!C3&C4);
S0=

(C1&!C2&!C3&!C4)| (!C1&C2&!C3&!C4)| (C1&C2&!C3&C4)|(!C1&!C2&!C3&C4)|
(C1&!C2&C3&C4)| (!C1&C2&C3&C4)| (C1&C2&C3&!C4)| (!C1&!C2&C3&!C4);

PLA Magic Daigram