The Three Stages
The strategy implemented in the Lindsey-Fox algorithm is organized in three stages. The first evaluates the polynomial over a grid on the complex plane and conducts a direct search for potential zeros. The second stage takes these potential zeros and “polishes” them by applying Laguerre’s method to bring them close to the actual zeros of the polynomial. The third stage multiplies these zeros together or “unfactors” them to create a polynomial that is verified against the original. If some of the zeros were not found, the original polynomial is “deflated” by dividing it by the polynomial created from the found zeros. This quotient polynomial will generally be of low order and can be factored by conventional methods with the additional, new zeros added to the set of those first found. If there are still missing zeros, the deflation is carried out until all are found or the whole program needs to be restarted with a finer grid. This system has proven to be fast, accurate, and robust on the class of polynomials with real, random coefficients and other similar, well-conditioned polynomials.
The Lindsey-Fox program can be outlined by:
Stage one: the grid search for prospective zeros
Construct a polar coordinate grid on the complex plane from the degree of the polynomial being factored
Use the FFT to evaluate the polynomial at each node along the concentric circles of the grid.
Search over each 3x3 set of values for relative minima. They are prospective zeros by the Minimum Modulus Theorem of complex analysis.
Stage two: polish the prospective zeros
Apply Laguerre’s algorithm to each prospective zero, correcting it to a better approximation of the “true” zero
Test the set of polished zeros for uniqueness and discard any duplicates to give a set of candidate zeros
Stage three: Unfactor, perhaps deflate, and verify
Unfactor the polished zeros i.e., reconstruct a candidate polynomial in coefficient form from the polished candidate zeros
If the degree of the reconstructed polynomial is the same as that of the original polynomial and differences in their coefficients are small, the factoring is finished
If some zeros were missed, deflate and factor the quotient polynomial. If that does not find all of the missed zeros, deflate and factor again until all are found or until no new ones are found
If deflation finds all the zeros that it can, and it still has not found them all, design a new grid with a finer spacing and return to stage one. If four restarts do not find them all and/or the reconstruction error is not small, declare failure.
Description of the three stages
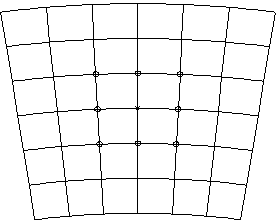
Stage one is the reason this algorithm is so efficient and is what sets it apart from most other factoring algorithms. Because the FFT (fast Fourier transform) is used to evaluate the polynomial, a fast evaluation over a dense grid in the complex plane is possible. In order to use the FFT, the grid is structured in polar coordinates. In the first phase of this stage, a grid is designed with concentric circles of a particular radius intersected by a set of radial lines. The positions and spacing of the radial lines and the circles are chosen to give a grid that will hopefully separate the expected roots. Because the zeros of a polynomial with random coefficients have a fairly uniform angular distribution and are clustered close to the unit circle, it is possible to design an evaluation grid that fits the expected root density very well. In the second phase of this stage, the polynomial is evaluated at the nodes of the grid using the fast Fourier transform (FFT). It is because of the extraordinary efficiency and accuracy of the FFT that a direct evaluation is possible. In the third phase of this first stage, a search is conducted over all of the 3 by 3 cells formed in the grid. For each 3 by 3 cell (see Figure below), if the value of the polynomial at the center node of the cell (the "x") is less than the values at all 8 of the nodes on the edges of the cell (the "o's"), the center is designated a prospective zero. This rule is based on the “Minimum Modulus Theorem” which states that if a relative minimum of the absolute value of an analytic function over an open region exists, the minimum must be a zero of the function. Finally, this set of prospective zeros is passed to the second stage. The number is usually slightly larger than the degree because some were found twice or mistakes were made. The number could be less if some zeros were missed.

Figure: Section of the polar coordinate grid showing a 3 by 3 cell
Stage two is more traditional that the other two. It “polishes” each of the prospective zeros found by the grid search. The first phase consists of applying an iterative algorithm to improve the accuracy of the location found by the grid search. In earlier versions of the program, Newton’s method was used but analysis and experiment showed that Laguerre’s method was both more robust and more accurate. Even though it required more calculation than Newton’s method for each iteration, it converged in fewer iterations. The second phase of the second stage checks for duplications. A “fuzzy” uniqueness test is applied to each zero to eliminate any cases where on two or more prospective zeros, iterations converged to the same zero. If the number of unique, polished zeros is less than the degree of the polynomial, deflation later will be necessary. If the number is greater, some error has occurred. This stage consumes the largest part of the execution time of the total factorization, but it is crucial to the final accuracy of the roots. One of the two criteria for success in factoring a polynomial is that each root must have been successfully polished against the original polynomial.
Stage three has several phases and possible iterations or even restarting. The first phase of the third stage takes all of the unique, polished zeros that were found in the first two stages and multiplies them together into the coefficient form of a candidate polynomial (“unfactors” the zeros). If the degree of this reconstructed polynomial is the same as that of the original polynomial and if the difference in their coefficients is small, the factorization is considered successful. Often, however, several zeros were missed by the grid search and polish processes of stage one and two, or the uniqueness test discarded a legitimate zero, so the original polynomial is “deflated” (divided) by the reconstructed polynomial and the resulting (low degree) quotient is factored for the missing zeros. If that doesn’t find them all, the deflation process is repeated until they are all found. This allows the finding of multiple roots, even if some of them were discarded earlier. If, in the unusual case, these further iterations of deflation do not find all of the missing zeros, a new, finer grid is constructed and the whole process started again at stage one.
Multiple order and clustered roots are unusual in random coefficient polynomials. But, it they happen or if factoring a non-random coefficient polynomial is attempted, the roots will be found with the Lindsey-Fox program in most cases but with reduced accuracy. If there are multiple order zeros (Mth order with M not too high), the grid search will find them, but with multiplicity one. The polishing will converge to the multiple order root but not as fast as to a distinct root. In the case of a cluster with Q zeros that fall within a single cell, they are erroneously identified as a single zero and the polishing will converge to only one of them. In some cases, two zeros can be close to each other in adjacent cells and polish to the same point. In all of these cases, after the uniqueness test and deflation, the quotient polynomial will contain a M-1 order zero and/or Q-1 zeros clustered together. Each of these zeros will be found after M-1 or Q-1 deflations. There can be problems here because Laguerre’s polishing algorithm is not as accurate and does not converge as fast for a multiple zero and it may even diverge when applied to tightly clustered zeros. Also, the condition of the quotient polynomial will be poorer when multiple and clustered zeros are involved. If multiple order zeros are extremely far from the unit circle, the special methods for handling multiple roots developed by Zhonggang Zeng [5] are used. Zeng’s method is powerful but slow, and hence only used in special cases [6].
Successful completion of the factoring of a polynomial requires matching zeros on the complex plane measured by the convergence of Laguerre’s algorithm on each of the zeros. It also requires matching the polynomial reconstructed from the found zeros with the original polynomial by measuring the maximum difference in each coefficient.