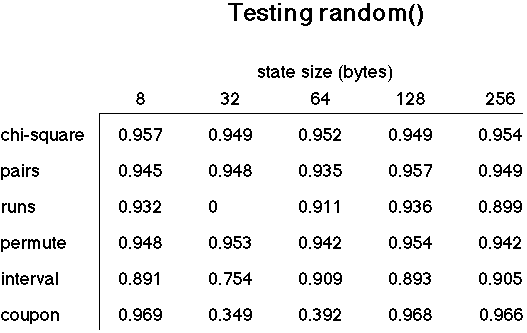
The interval test results are for bits 30-27 of the value returned by random(). This corresponds to a gap test in which the values are grouped into 16 sets. The coupon collectors test results are for bits 30-28, corresponding to 8 distinct values. All other tests use the full 31-bit number generated by random(). Each test used a critical value for a 0.95 probability, which means that if random() produces truly random uniformly distributed values, it should pass each test 95% of the time.

Okay, why does random() appear to behave so badly for the run-length test with 32 bytes of state? This is a case where appearances may be misleading. Most of the runs are short; out of about 582,000 runs, almost 99.1% of the runs are of length 4 or shorter. The expected counts for runs of these lengths match closely the observed counts. Large relative differences (say, 1% or larger) occur only for the longer run lengths, particularly 5 and 6. However, even though they account only for about 0.9% of the total number of runs, they are sufficient to cause the entire set of observations to fail the chi-square test.

The zero passing rate is real - random() never passed out of 1000 tries. Whether or not this is likely to be a problem depends on how sensitive your application is to an over-production of length 5 runs and an under-production of length 6 runs. It seems doubtful that this will be significant in most applications.

For more information on each test, see

• chi-square test
• pairs test
• run-length test
• interval test
• permutation test
• coupon collectors test

Return to the testing home page.