ELEC 241 Lab

Experiment 5.1

Measuring a Signal's Spectrum

Part A: The Spectrum of a Sine Wave

The spectrum of a sine wave should be pretty boring. By definition it consists of a single component at the fundamental frequency whose amplitude is equal to the amplitude of the waveform. Nevertheless, it is useful being able to see the amplitude and frequency in a single picture, as well as being able to assess how "pure" (i.e. how truly sinusoidal) the purported sine wave actually is.


Step 1:

 Connect the cable from the DAQ card to J3-1 on the rightmost interface module.

Step 2:

 Connect the output of the function generator to CH1 of the scope and to A/D input 4 (pin 46 on the bottom interface board socket connector).

Step 3:

 Set the function generator to produce a 2 V p-p, 500 Hz sine wave.

Step 4:

 Download Lab5_Spectrum_Analyzer and open in Labview. Set "number of samples per channel" and "rate" to 10000. Set "averaging mode" to RMS averaging.

Step 5:

 Start the instrument by selecting Run from the Operate menu, or by pressing the run button (the small arrow just below the menu bar). The instrument is divided into a display area (the large black area on the left with green lines and text) and a control area (the gray area on the right). For now, let's concentrate on the display area. It should look something like this:
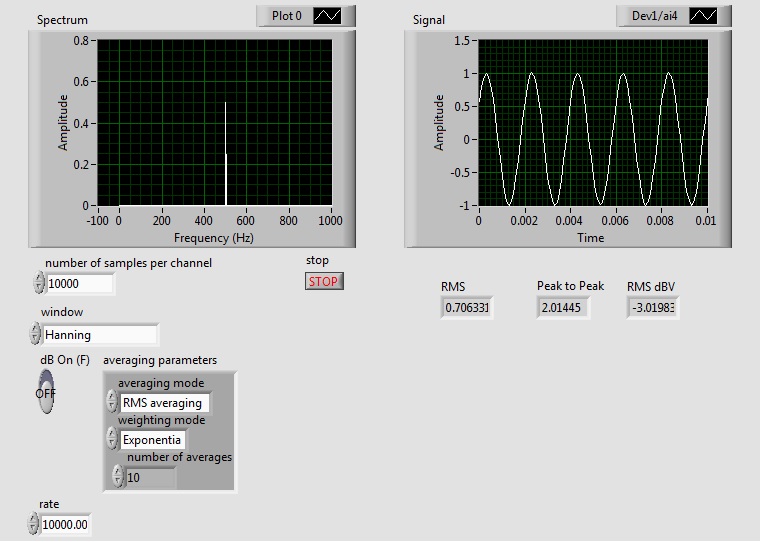
The top portion is the waveform display. It should be showing a sine wave, just like the scope.

Step 6:

 There is some additional information about the signal just above the waveform display. The line labeled "Signal Amplitude" gives three different measurements of the signal amplitude: Vrms: the RMS voltage, dBV: the RMS voltage in decibels relative to 1 V, and Vp-p: the peak-to-peak voltage.

Vary the function generator AMPLITUDE control and verify that these values change appropriately.

Step 7:

 Disconnect the function generator. What remains is a noise signal which is being generated within the rest of the system. In this case it has both a random component (the grass) and a periodic component (the 3.3 kHz signal).

Step 8:

 Reconnect the function generator. Vary the frequency and observe how the spectrum display changes.

Part B: The Spectrum of Triangle and Square Waves



Step 1:

 The Fourier series of a triangle wave has only odd harmonics, which fall off as \(1/n^2\) (12 dB/octave). Set the function generator to produce a triangle wave and see if this is the case. Are there any even harmonics? If so, why are they there? What happens when you vary the duty cycle?

Step 2:

 The square wave also consists only of odd harmonics, but falling off as 1/n (6 dB/octave). Set the function generator to square wave and observe the spectrum. Vary duty cycle. Depending on the exact frequency you may see a number of extraneous harmonics. These are due to the phenomenon of aliasing which we will examine in Lab 6.

Step 3:

 The spectrum analyzer labeled "Spectrum" displays magnitude on and frequency on a linear scale. It is sometimes useful to view the spectrum on a semi-log or log-log plot. Stop executing the program, right-click on the spectrum display (gray area) and click on Properties->Scales. Select Log.

Adjust the amplitude if necessary to obtain a good display. Note the hyperbolic shape of the 1/n fall off in magnitude.

Step 4:

 Now get a log-log plot with magnitude in dB by changing the Y-scale to Log and setting a multiplier of 20 (under Scale Factors). Note that the 1/f fall off is now a "linear" 20 dB/decade slope.

Step 5:

 Switch the function generator to triangle wave. Is the slope now 40 dB/decade, as we expect? Set the spectrum analyzer back to linear display (both magnitude and frequency). Note the shape of the spectrum.

Step 6:

 Set the function generator to square wave. Set the Duty Cycle to 15%. You should now have a waveform consisting of narrow pulses. Note the shape of the spectrum. It should have the \(\sin(x)/x\) (sinc) shape we saw in class.

Step 7:

 Set the spectrum analyzer back to dB magnitude and log frequency. Set the duty cycle to 50%.

Part C: The Spectrum and Frequency Response



Step 1:

 Wire the following circuit:
\includegraphics[scale=0.650000]{ckt5.1.ps}

This is the same circuit we used in Lab 3, so you should have its transfer function in your lab notebook.

Step 2:

 Connect the output of the function generator to \(v_\text{in}\). Also connect CH1 of the scope and A/D input 4 to \(v_\text{in}\).

Step 3:

 Set the function generator to produce a 50 Hz sine wave at 1 Vrms (0 dBV).

Step 4:

 Move CH1 of the scope and A/D input 4 to \(v_\text{out}\).

Step 5:

 Increase the frequency of the function generator and observe the behavior of the spectrum display. The tip of the peak corresponding to the fundamental of the sine wave will trace out the magnitude of the transfer function of our circuit. Note that the two numbers above the spectrum display. They give the magnitude and frequency of the largest peak in the spectrum. The "Peak Frequency" readout should correspond to the frequency setting of the function generator.

Since the transfer function falls off as 1/f for high frequencies, we expect the output to fall 6 dB per octave for frequencies well above the cutoff frequency. Check the response at 1 kHz, 2 kHz, and 4 kHz and see how well this holds.

Step 6:

 Turn off the function generator.