ELEC 242 Lab

Background

Unlike our "ordinary" circuit elements (resistors, diodes, etc.) which are characterized by a fixed I-V relationship, the I-V relationship at the electrical port of a transducer changes depending on what is happening on its physical port.

Permanent Magnet DC Motors

An ideal DC motor looks like this schematically:

$\includegraphics[scale=0.650000]{motor1.ps}$ The current

flowing in the armature windings produces a mechanical torque $T_{dev}$ . In the other direction, if the shaft is rotating at angular frequency $\omega_m$ (in radians/sec) then a voltage

(called the back emf) is developed across the armature windings. These four quantities are related by the coupling equations $T_{dev} = K_t I_a$ and $E = K_e \omega_m$ .

Some texts (including Cogdell) state these equations as $T_{dev} = K_T\Phi I_a$ and $E = K_E\Phi \omega_m$ , to indicate the dependence of the torque and back emf on the strength of the magnetic flux ( $\Phi$ ) in the motor. In some types of DC motors (so called wound field motors) this flux may be changed by varying a second current, called the field current ( ). In a permanent magnet motor, $\Phi$ is fixed by the strength of the permanent magnets, so we will absorb the $\Phi$ into the constants (and use lower case subscripts) to simplify the equations.

Just like a real battery departs from ideal because of its internal resistance, a real motor also contains a resistance, called the armature resistance ( ) in series with an ideal motor. This gives the following circuit:

$\includegraphics[scale=0.650000]{motor2.ps}$

Now, although the armature current is still equal to the current flowing into the motor, the voltage across the motor terminals is no longer equal to the back emf . Instead we have, using KVL: . Combining this with the coupling equations for the ideal motor, we get:

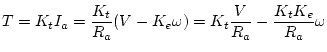
$\displaystyle V = R_a I_a + K_e \omega$ or $I_a = (V - K_e \omega)/R_a$ Substituting into the equation for torque, we get: $\displaystyle T=K_tI_a = \frac{K_t}{R_a}(V-K_e\omega) = K_t\frac{V}{R_a}-\frac{K_tK_e}{R_a}\omega$ Which gives the torque in terms of the applied voltage and the speed. Alternately, we could solve for $\omega$ in terms of

and

: $\displaystyle R_aT=K_t(V-K_e\omega)$
$\displaystyle \frac{R_aT}{K_t} = V-K_e\omega$
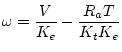
$\displaystyle \omega = \frac{V}{K_e} - \frac{R_aT}{K_tK_e}$

If we apply a voltage source to a motor with no mechanical load connected to it, then the torque produced by the current, $I_a=\frac{V}{R_a}$ , will act to accelerate the rotor of the motor. However, as the velocity $\omega_m$ increases, it produces a back emf which opposes the applied voltage. Thus, rather than continuing to accelerate indefinately, the motor reaches an equilibrium when $V=K_e\omega_{NL}$ where $\omega_{NL}$ is called the no load speed.

On the other hand, if we lock the rotor so that it can't turn (i.e. stall the motor) the current $I_a=\frac{V}{R_a}$ will continue to flow, producing the stall torque $T_s=K_t\frac{V}{R_a}$ . Stated another way, if a load greater than is required, the motor will stop, or stall.

For values of load torque between zero and , we have the relations given above. If we plot vs. $\omega$ for a fixed voltage , we get what is called a constant voltage speed-torque curve. If we change the voltage, the curve will move up or down, giving a set of speed vs torque relations, one for each voltage.

$\includegraphics[scale=0.650000]{speedtorque.ps}$

In reality, the load torque is never zero. There will be some friction in the bearings, aerodynamic drag on the rotor, etc. Also, some types of motors have preferred orientations or detents where the magnets try to hold the rotor at a particular angle. This gives rise to a ripple torque which varies depending on the angle of the shaft. This will cause us some difficulty when we try to measure the torque characteristics of our motor, and can cause no end of grief when trying to use a motor with this characteristic in certain applications (fortunately not in ours).