ELEC 243 Lab

Experiment 8.2

Active Filters

In the previous Experiment we converted a voltage divider, whose attenuation is independent of frequency, to a filter by replacing one of the resistors with a capacitor. If we substitute a capacitor for a resistor in the inverting op-amp circuit, we can effect a similar transformation from a constant gain amplifier to a filter where gain depends on frequency. We can analyze the response to sinusoidal signals by representing the input and feedback elements as impedances:

\includegraphics[scale=0.500000]{ckt7.3.1.ps}
Then the formula for gain ( $G=\frac{R_F}{R_1}$ ) becomes a formula for the transfer function: $H=\frac{Z_F}{Z_1}$ .

In this Experiment we will explore the result of using various components and combinations of components for $Z_1$ and $Z_F$ . Since we will be making a number of frequency response plots we will want to use the Labview "Transfer Function" program that we used in Experiment 8.1. Here is a diagram of the required connections:

\includegraphics[scale=0.500000]{ckt7.3.7.ps}
UUT is EE jargon for Unit Under Test, in this case our op-amp filter circuit.

Part 1: Low-Pass Filter

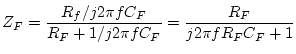In the circuit below the feedback element has impedance $\displaystyle Z_F=\frac{R_f/j2\pi f C_F}{R_F+1/j2\pi f C_F}=\frac{R_F}{j2\pi f R_FC_F+1}$ . Since $Z_1=R_1$ we have $H(f)=\frac{Z_F}{R_1}=\frac{R_F}{R_1}\frac{1}{1+j\frac{f}{f_c}}$ where $f_c=\frac{1}{2\pi R_FC_F}$ . If we plot $\vert H\vert$ as a function of $f$ we find that the transfer function of this circuit is a low-pass filter with a passband gain of $R_F/R_1$ and a cutoff frequency of $f_c$ .
\includegraphics[scale=0.500000]{ckt7.3.8.ps}
Fig. 7.3: Active Low-Pass Filter


Construction:

 Wire the circuit of Fig. 7.3 using $R_1=R_F=\rm 2.2 k\Omega$ and $C_F=\rm0.33 \mu F$ .

Testing:

 Verify that the circuit works using the function generator as an input.

Characterization:

 Using the Labview transfer function VI, measure and record the frequency response between 20 Hz and 2 kHz.

Part 2: High-Pass Filter

By placing the capacitor in the input network we can make a high-pass filter:

\includegraphics[scale=0.500000]{ckt7.3.2.ps}
Fig. 7.4: Active High-Pass Filter
A similar analysis shows that this filter has a passband gain of $R_F/R_1$ and a and a cutoff frequency of $f_c=\frac{1}{2\pi R_1C_1}$ . This is the same circuit we used for the second stage of the photodiode amplifier last week.


Construction:

 Wire the circuit of Fig. 7.7 using $R_1=R_F=\rm 2.2 k\Omega$ and $C_1=\rm0.33 \mu F$ .

Testing:

 Optional. If you're confident of your wiring, proceed to the next step, otherwise test with function generator and oscilloscope.

Characterization:

 Using the Labview transfer function VI, measure and record the frequency response between 20 Hz and 2 kHz.

Part 3: Bandpass Filter

We could combine the high-pass input network with the low-pass feedback network to make a band-pass filter.

\includegraphics[scale=0.500000]{ckt7.3.3.ps}
Fig. 7.5: Broadband Bandpass Filter
We can a much narrower bandwidth by incorporating an inductor:
\includegraphics[scale=0.500000]{ckt7.3.4.ps}
Fig. 7.6: LC Bandpass Filter
Taking into account the internal resistance of the inductor this circuit would be more accurately drawn as:
\includegraphics[scale=0.500000]{ckt7.3.5.ps}
Fig. 7.7: RLC Bandpass Filter


Construction:

Wire the circuit shown in Fig. 7.7 using $C_1=\rm0.33 \mu F$ , $L_1 =\rm 18mH$ and $R_F=470\Omega$ . Note that $R_1$ shown in Fig. 7.8 is the internal resistance of the inductor and not a spearate component. Before installing the inductor measure its resistance with your DMM and be sure to take it into account when analyzing the circuit.

Testing:

 Optional again.

Characterization:

 Measure and record the frequency response between 60 Hz and 6 kHz. Because of the sharpness of the peak in the frequency response, you should use a larger number of steps, say 40.

Question 2:

 Analyze the three circuits used in this Experiment and compare the calculated frequency response with that which was observed. For the low-pass and high-pass filters, compare your results with the corresponding circuits from Experiment 8.1.