ELEC 243 Lab

Experiment 9.1

Filtering with Labview

The analog filters we looked at last week have the advantage of simplicity and low cost, but they also have relatively low performance. Much higher performance analog filters are possible, but they are correspondingly more complex, and difficult to construct. Digital filters are capable of much higher performance, and since we already have Labview up and running, most of the construction is already done. The one caveat with digital filters is that we have to be careful to avoid aliasing.

Part 1: A Built-in Anti-alias Filter

Most of the work we will be doing this week will involve the optical emitter-detector pair we have been building over the past two weeks. Rather than using the stand-alone filter we built last week in Part 3 of Experiment 8.3, we can build the anti-aliasing filter into the photodiode amplifier, resulting in a simpler circuit. We can do this by adding a capacitor in parallel with the feedback resistor in the second stage of the photodiode amplifier, converting the existing high-pass filter into a bandpass filter.
\includegraphics[scale=0.500000]{ckt7.1.6.ps}
Fig. 7.1: New Photodiode Amplifier


Construction:

 Add a 1 nF capacitor to your photodiode amplifier as shown in the circuit above. Remove the 4.7 kΩ resistor and .033 µF capacitor used in last week's filter and connect $v_{photo2}$ directly to ach4.

Testing

 Start the "Spectrum" VI and verify that things still behave the same as they did at the end of last week's Lab.

Part 2: Continuous Signals in Labview

Although we created a few continuous signals with Labview in Part 3 of Experiment 4.1, all of our measurements have been based on single input values or fixed sized blocks of inputs. Filtering, like we did last week in Lab 8, is a continuous process which operates on a stream of input samples to produce a corresponding stream of output values. Although we may divide this stream into blocks for convenience in processing, they must be smoothly stitched together so that no discontinuities are present in the output.

Let's start by building a VI that simply copies a continuous input stream to a continuous output stream, i.e. a Labview wire. We can do this by putting a A/D converter block and a D/A converter block inside a while loop and connecting the A/D output to the D/A input.


Construction:

 Start Labview and build a new VI with the following block diagram:
For the input (A/D DAQ Assistant) select Analog Input and Voltage, then set
Physical Channel ai4
Input Range $\pm 10\rm V$
Terminal Confituration RSE
Acquisition Mode Continuous
Samples to Read 8192
Rate (Hz) 100000

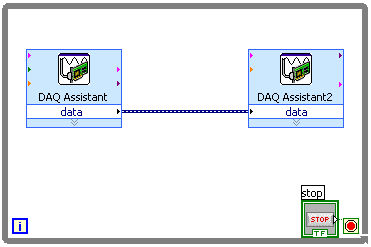
For the output set Analog Output and Voltage, then

Physical Channel ao0
Output Range $\pm 10\rm V$
Acquisition Mode Continuous

Also check the "Use timing from waveform data" box.

Setup:

 We are going to apply our Labview filters to the photodiode amplifier output. Since we now have a built-in anti-aliasing filter we can connect the photodiode amplifier directly to the Labview A/D input, as shown in the following diagram.
\includegraphics[scale=0.500000]{ckt7.1.7.ps}

We will assess the results of our filtering by a number of means, including watching and listening, so connect the Labview D/A output to CH2 of the oscilloscope and to the handset earpiece. As inputs, plug in the microphone and connect the function generator to $v_{fg}$ on the microphone mixer.

Testing:

 Turn everything on and start the VI. Speak into the microphone and play with the function generator. You should be able to hear the sounds in the earpiece and see them on the oscilloscope, just as you did last week in Part 5 of Experiment 6.3.

When everything is working correctly, save your VI as "wire.vi".

Part 3: A Labview Filter

Once we have the Labview wire working correctly, we can convert it into a Labview filter by inserting the appropriate filter blocks between the A/D block and the D/A block.


Construction:

 Remove the wire between the A/D DAQ Assistant block and the D/A block. Place a Filter block (located in the Analysis palette of the Functions popup) between the two. In the Configure Filter dialog, accept the defaults (for now). Connect the D/A data output to the filter Signal input and connect the Filtered Signal output to the A/D datainput.

If your blocks are very close together, Labview may try to automatically make connections for you. In particular, it may connect the error out of one block to the error in of the adjacent block, using a pink wire. If it makes automatic connections that you don't approve of, simply remove them.

When you get done, it should look like this: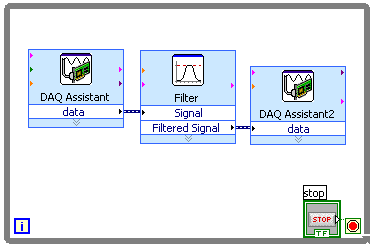



Testing:

 Perform the same tests as in the previous Part. Because of the fairly aggressive filtering the sound will be rather muffled.

Part 4: A Switchable Filter

With our current VI, we can filter the signal, but it's difficult to assess the results since we can't easilly compare the filtered output with the original input. However, with Labview it's easy to add a switch to allow us to select either the filtered or unfiltered signal.


Construction:

 The first thing we need is a switch. Go to the front panel and select an appropriate one from the Buttons and Switches palette (press the Buttons button on the Controls popup). Change the label to something meaningful like "Filter On."

Return to the block diagram and move the new icon (a green box with a picture of your chosen switch in it) to a position below the filter block. From the Functions popup select Comparison then Select. Place the resulting icon to the right of the switch icon. The select block has three inputs and one output. The middle input is the selector: connect it to the switch. (The resulting green wire indicates a boolean signal.) Connect the output to the data input of the D/A block. Connect the upper input to the filter output and the lower input to the A/D output.

Here's what you should have: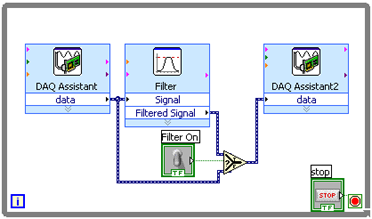



Testing:

 Fire everything up and listen to the earpiece while flipping the filter on/off switch back and forth. You should be able to hear the difference between filtered and unfiltered.

Observations:

 With the default values for the filter block (100 Hz lowpass) the noise at the output of the filter will be less than the noise at the input, but so will the signal. Have your lab partner speak into the microphone and try various combinations of filter in vs. filter out, under-shelf florescent light on vs. off, etc. Is the speech intelligible with the filter turned on?

We can reduce the amount of damage to the speech signal by increasing the bandwidth of the filter. To do this, stop the VI, double click on the filter block, enter a new value for Cutoff Frequency, and click OK. Try several different values and report on the results.

Part 5: An Assortment of Labview Filters

From our observations last week, we might suspect that a highpass filter would be more effective that a lowpass in reducing noise from the flourecent lamp without doing too much damage to the speech signal. We could test this by editing the filter block again, this time changing the filter type as well as cutoff frequency. It would be a lot more convenient if we could make such changes while the VI was running. While we're at it, why not display the spectra of the input and output signals. Rather than add all these useful features one by one, let's cut to the chase and use a prefabricated VI that already has them.


Setup:

 Load the "Filters" VI from the ELEC 243 Start menu. It has the same connections as the VIs in previous Parts, so no rewiring is necessary. The under-shelf florescent lamp should still be on to provide a source of noise to be filtered.

Operation:

 As promised, this VI has a number of new goodies. Most prominant are the four graph displays. The top two show the input waveform and spectrum and the bottom two show the filtered output. Underneath the waveform displays is a slider to adjust the time scale. The Full Range button overrides the slider and displays the entire signal. Similarly the slider and button under the spectrum displays control the displayed frequency range.

The selection of filter type and adjustment of filter parameters are under control of the tab control in the center left of the front panel.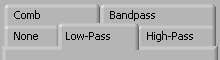

Selecting one of the tabs selects the corresponding filter and displays sliders for cutoff frequency, bandwidth, etc. The switch above the tab panel selects whether the D/A converter is connected to the unfiltered input or the filtered output.

Finally there are two numeric indicators which show the RMS value of the input and output signals. These can be used in computing SNR.

Inside the VI:

 Open the block diagram by selecting Show Block Diagram from the Window menu. The overall structure is similar to the VI from the previous Part, but includes displays similar to those of the Spectrum VI. One important addition is that the various filters are selected by a case block rather than a selector block. The case block is the equivalent of a case statement in conventional programming languages. Only the functions in the selected page are executed, the contents of the other pages are ignored. The selection is determined by the value on the selector input, which in this case is connected to the tab control icon. To view the different pages, place the cursor over the text field at the top of the block. The cursor will turn into a finger. Left click and select the desired page from the list.

Testing:

 Select None from the filter selection tab control and start the VI. The input signal (microphone plus function generator) should be heard in the earpiece and seen on the oscilloscope. The signal and its spectrum should also appear in the displays on the VI front panel. If necessary, adjust the Time Scale slider to give a suitable display.

Filtering:

 Select Lowpass from the filter selection tab control. Adjust the cutoff frequency while listening and watching the displays. Is the behavior what you would expect based on the results of the previous Part?

Now try the highpass filter. Again adjust the cutoff frequency while observing and listening. Is this more effective than the lowpass filter in improving the quality of the output signal?

A Comb Filter:

 Although much of the power in the noise signal is concentrated at low frequencies, it has significant harmonics extending up to several kilohertz. This means that the spectra of the signal (speech) and noise (buzz) overlap and we can't use high-pass, low-pass, or bandpass filters to separate them. However, these harmonics are at known, fixed frequencies. If we had a filter which would block multiples of 60 Hz and pass all other frequencies, we should be able to remove the noise from speech signals without doing too much damage to the latter.

Fortunately there is a simple filter, called a comb filter, which does exactly that. It works by subtracting a delayed version of the signal from the original input. Periodic signals whose period is an integer submultiple of the delay are cancelled.

Select Comb from the filter selection tab control. Most of the buzz should disappear, both from the output spectrum and the handset earpiece. Adjust the Comb Delay value to minimize the remaining buzz.

Unplug the microphone and adjust the function generator to produce a 1 kHz sinewave of comfortable listening volume. Slowly increase the frequency to about 2 kHz. What happens?

Question 1:

 Compute the frequency response of the comb filter and show that sinusoids whose periods are an integer submultiple of the delay are in fact blocked by the filter. What is the response to a sinusoid of frequency 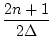$\displaystyle \frac{2}{(2n+1)\Delta}$ where $\Delta$ is the delay and $n$ is an integer?

Part 6: Narrowband Signaling

With the comb filter we were able to match the characteristics of the filter with those of the noise, rejecting the noise and passing everything else, hopefully including the desired signal. If we have a signal with well defined characteristics, we can do the reverse: match the filter with the signal and hope that it adequately rejects the noise.

This is difficult to do with speech, whose spectrum is constantly changing, but if we can convey our information with a fixed frequency signal, we can use a narrowband bandpass filter to extract it from the noise.


Setup:

 With the filter selector still set to Comb, set the function generator to produce a 2 kHz sine wave. Adjust the frequency slightly to maximize the filter output.

Temporarily disconnect the function generator. With the under-shelf florescent lamp on, measure the RMS value of the signal at the input of the filter. Record this value as $V_{N2}$ . Turn the lamp off and record the resulting RMS value as $V_{N1}$ . This should be significantly less than $V_{N2}$ .

Set the filter selector to None. Reconnect the function generator and adjust the function generator amplitude so that the Output RMS value is approximately equal to $V_{N2}$ . Record this value as $V_S$ . Since $V_{N1}\ll V_{N2}$ , this will serve as our estimate of the noise-free signal amplitude.

SNR with no Filter:

 Turn on the under-shelf florescent lamp. Since $V_S \approx V_{N2}$ the signal to noise ratio will be approximately one. Observe the signals, spectra, and RMS values for the input and output. Record the output RMS value as $V_{SN}$ . Is there a meaningful relationship between this number and $V_S$ and $V_{N2}$ ?

SNR with Various Filters:

 For each of the four filters, estimate the SNR using the same measurements performed in the "Setup" step, i.e. disconnect the function generator to measure $V_{N2}$ , then reconnect the function generator and turn off the under-shelf lamp to measure $V_S$ . Compute the SNR and express your result in dB. For the highpass and lowpass filters, adjust the cutoff frequency to give the cleanest looking output signal. For the bandpass filter, set the center frequency to the function generator frequency and the bandwidth to 200 Hz.

Question 2:

 Summarize the results of your filtering experiments. Suggest which combinations of filter type and frequency would be appropriate for various types of signals and noise.