ELEC 243 Lab

Experiment 9.2

Binary Signals

A/D conversion allows us to present Labview with an accurate, digital representation of an analog signal. In some cases this is too much of the wrong information. If we want to know if the lights are turned on or off (a two-valued or binary signal), knowing the illumination level in lux (a continuous variable) is not necessarily useful. However, if we also know the illumination level when the lights are off ($E_0$ ) and when they are on ($E_1$ ) we can compare the measured illumination level with an appropriate threshold (e.g. $(E_0+E_1)/2$ ) to make a decision. We can use the same approach to decide if someone or something is standing between an optical source and detector.

This is a simple example of extracting digital information from an analog signal by converting it to a binary signal. We can extract additional information from the timing or structure of the patterns of on and off. For example, we can determine when, how often, or for how long an object interrupts our light beam. Or we can transmit arbitrary messages from one end of the beam to the other by turning it on and off in a structured pattern (like the morse lanterns of pre-wireless ships).

Part 1: Simple Thresholding

We'll start by looking at what happens when we subject our photodiode output to the simple thresholding process described above.


Building the VI:

Reload the "wire.vi" file that you saved in Part 2 of the previous Experiment. On the front panel, place a Waveform Graph indicator by selecting Graph Inds, then Graph from the Controls popup. On the block diagram, remove the wire between the A/D block and the D/A block. Remove the D/A block and replace it with the icon from the Waveform Graph.

From the Functions popup, select Arith/Compare, then Comparison, then Greater Than 0?. Place the resulting component between the A/D block and the Waveform Graph block. Connect the input of the >0 symbol to the A/D output and connect its output to the input of the waveform graph. Here's what you should have: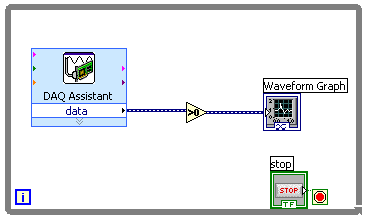



Preliminary Testing:

 Turn off the under-shelf lamp to minimize the amount of noise in the signal. Set the function generator to produce a 20 Hz sine wave and adjust the amplitude to produce a 1 V p-p waveform at $v_{photo2}$ .

Start the VI. The waveform graph should display a 20 Hz waveform having values of 0 and 1. You can make the display easier to interpret by changing the Y-axis scale. Turn off auto-scale by right clicking over the display and selecting AutoScale Y. Double click on the "1" at the top of the y-axis scale and enter "2". Enter "-2" as the lower limit. You should now be able to clearly see the tops and bottoms of the square wave.

Viewing Input and Output Together:

 It would be nice to be able to see the original analog input as well as the binary output. We could add a second waveform graph to the front panel and connect it to the A/D output. We can also display both signals on the same graph by combining them into a two signal vector, like we saw in Lab 4. We can do this by using the reverse of the Split Signals block, called Combine Signals.

Stop the VI and go to the block diagram. Remove the wire between the >0 symbol and the waveform graph icon and place a Combine Signals block in the resulting space (it's next to the Split Signals block in the Sig Manip palette). Connect its output to the waveform graph, its upper input to the A/D output, and its lower input to the >0 output. When you're done it should look like this: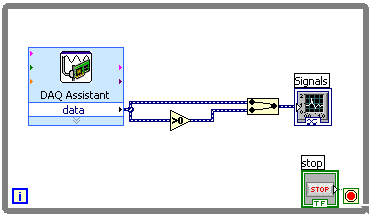

Restart the VI. You should now see both signals, one in white and the other in red.

A Variable Threshold:

 The >0 block compares its input with a fixed thershold of zero. This is fine for converting sine waves to square waves, but in general we would like to be able to adjust the threshold to suit our requirements. Fortunately this is easy to do.

On the front panel, place a vertical slider and set the limits to 1 and -1. On the block diagram remove the >0 symbol and replace it with a Greater ? block. Connect its upper input and output to the dangling wires where the >0 block was removed. Connect its lower input to the output of the slider's icon. Restart the VI and verify that you can now adjust the comparator threshold.

Part 2: An Optical Interrupter

Now that we have the ability to produce binary signals from analog signals, lets use it to detect the presence of objects in the gap of our emitter-detector pair. Since the presence of such an object blocks or interrupts the path of light, an emitter-detector configuration used in this manner is sometimes called an optical interrupter.


Connections:

 Since the state (blocked or unblocked) of the beam is a DC signal, we will need to bypass the DC blocking function in our photodiode amplifier. The easiest way to do this is to connect the A/D input to the output of the first stage of the amplifier, $v_{photo1}$ :
\includegraphics[scale=0.500000]{ckt7.2.3.ps}

Since we need a constant intensity light beam, disconnect the function generator from the microphone mixer.

Testing:

 With your circuit rewired as shown above, turn everything on. Measure the value of $v_{photo1}$ with the beam unobstructed and with it blocked by an opaque object (such as your finger). Compute the average of these two voltages and set the comparator threshold to the resulting value. Observe the waveform graph and verify that the comparator output corresponds to the blocked/unblocked status of the beam. Compare the behavior when the object is moved quickly through the beam and when it is moved very slowly.

Part 3: Handling Noisy Signals

You may notice multiple transitions between 0 and 1 as the object enters and leaves the gap. This is due to the fact that the beam is not blocked instantaneously. When $v_{photo1}$ approaches the threshold value, the noise on the signal results in multiple crossings of the threshold during the transition. If all we want is a static indication of blocked or unblocked this may not be a problem, but if we are counting the number of times something passes across the beam, it's a very serious problem.

There are a number of things we could do. Since we are now experts on filtering, we could filter the signal. Another approach is to use a Schmitt trigger which automatically switches between two thresholds depending on whether the signal is increasing or decreasing. If the spacing (or hysterisis) between these two levels is greater than the amplitude of the noise, only the larger excursions caused by the signal will result in changes in the output.

Rather than build up this new functionality bit by bit, we'll once again take advantage of an existing Labview program which already has it installed.


Setup:

 Stop the current VI and load the "Binary" VI from the ELEC 243 program menu. This VI has the same connections, so no rewiring is necessary.

Testing:

 Select None from the filter select tabs (the upper set) and Threshold from the lower set of tabs. Set the threshold to the same value used in the previous Part. Start the VI and observe that the behavior is the same. (To allow for smaller input signals, this VI uses separate graphs for input, filtered input, and output.)

Schmitt Trigger:

 Select Schmitt from the comparator tabs. Set the threshold to the same value as the previous step and set Hysterisis to approximately 25% of the threshold value. This should result in cleaner transitions of the output waveform, independent of the speed of the object.

Observations:

 Experiment with various combinations of filter and comparator, filter parameters and threshold values, fast and slow motion, etc. Summarize the results of your experiments.

Part 4: Binary Signals

In the comparator VI we built in Part 1, the output of the >0 block had the same dark blue striped code as the input, i.e. they were both dynamic data signals. While this makes the comparator output easy to display, it's less useful for other purposes. As we have seen, Labview uses the binary or boolean data type to control logical operations. If we want to use the output of the threshold detector to drive decisions elsewhere in a Labview program, it must be converted to the boolean data type.

This conversion could be applied after the comparison, using a From DDT block as we did before, with the output type being a binary vector. Alternately, we could convert the dynamic data type to an ordinary, floating point vector before the comparator. When the inputs to a comparator are ordinary data types, the output is automatically binary.


Inside the Binary VI:

 Open the block diagram of the Binary VI. It is similar to the Filters VI, but it has an additional case statement block to select the comparison method. Note the conversion from dynamic data to vector type between the two case statements.

Sub-VIs:

 Examine the pages of the right-hand case statement. The Threshold page is similar to what we constructed in Part 1, but the Schmitt block contains a magic box labeled "S.T." (for "Schmitt Trigger"). This is a sub-vi, a connection of blocks and connections that have been moved to a separate file to reduce clutter in the main VI and to allow convenient reuse. To see what's inside, simply double click over the box.

The Schmitt Trigger VI:

 Connections to sub-VIs are made via controls and indicators, so the front panel of the Schmitt trigger indicates its input/output structure. There are three inputs (signal, threshold, and hysterisis) and one output (binary signal).

The block diagram is somewhat more interesting. We can see the icons corresponding to the input and output terminals, but the main feature is the strange looking block containing the functional blocks. This is a for loop.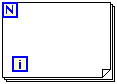

This is similar to a while loop in that it repeatedly executes its contents. However, instead of looping until a specified condition is met, it loops for a fixed number of times (the N in the upper left corner).

When a signal passes between the outside and inside of a block, the point of penetration is called a tunnel, denoted by the small square on the border of the block. When an input (or output) to a for loop is a vector, it exhibits a useful property called auto-indexing. In this case, the loop limit (N) is taken from the dimension of the vector, and on the inside of the loop, the value of each signal is the i-th component (a scalar) rather than the entire vector. This allows us to do point-by-point operations on a vector.

Another useful property of a for loop is the ability to pass a value from one iteration of the loop to the next. This is done by using a shift register, denoted by a small rectangle with an upward pointing arrow on the right hand border and a corresponding node with a downward pointing arrow on the left border.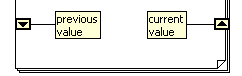

The value present at the right hand terminal of a shift register will appear at the matching left hand terminal during the next iteration.

Observations:

 Examine the S. T. VI and convince yourself that it does indeed implement a comparator with hysterisis.

Part 5: Modulated Signaling

If the amplitude of the noise is small compared to the difference between the blocked and unblocked photodiode output, the techniques described above will work reliably. This is the case for our optical interrupter, where the distance between the emitter and detector is small compared to the distance to the sources of interference. However, as we increase the separation between emitter and detector, the amplitude of the signal from the emitter will decrease while that from the interference will remain the same. Eventually the system will fail.

The way to improve the situation is to increase the signal to noise ratio. Since the signal characteristics of the noise are fixed, we should choose an emitter signal that can be successfully separated from the noise by filtering. In our situation, most of the noise is due to ambient lighting. For some sources, this includes a strong periodic component at multiples of 60 Hz, but in all cases it includes a significant DC component. This means the signal from the emitter should be at a high frequency, preferably an odd multiple of 30 Hz.

If we use an AC signal for the emitter signal, we can no longer compare the received signal from the detector to a threshold to determine if the beam is blocked or unblocked. If we did, it would appear that it was being interrupted at the modulating frequency. Instead, we need to apply the threshold to the amplitude of the filtered detector waveform. There are a number of ways we can determine this amplitude. The simplest is to simply take the absolute value and smooth the result with a low pass filter. This is the same process used to receive AM radio stations, and is called envelope detection.


Setup:

 Reconnect the A/D input to $v_{photo2}$
\includegraphics[scale=0.500000]{ckt7.2.4.ps}

Set the function generator frequency to the value determined in Part 6 of Experiment 9.1. Set the filter tab to AM. Set the Frequency slider to the function generator frequency and the Bandwidth to 200 Hz. Measure the Output RMS with the beam blocked and unblocked and set the Threshold halfway between the two values.

Testing:

 Verify that the Output corresponds accurately to the blocked/unblocked state of the beam.

Observations:

 Simulate increasing distance between the emitter and detector by reducing the function generator output. Adjust the Threshold appropriately. How low can you get and still achieve reliable operation? To what increase in distance does this correspond?

Part 6: Extracting Data from Binary Signals

In some cases all we need to know is whether or not something is positioned between the emitter and detector or the optical interrupter. However, sometimes we need to know more quantitative information. For example, how long was it there, how many times was it there, etc? We can get this information by counting the output pulses, measuring their width, etc.

Labview provides several VIs for working with pulses which can tell us things such as their rate and width. Other functions, such as counting pulses, we will have to build ourselves. One such VI, which counts the number of 0-to-1 transitions, has been built and installed in the Process program. Its results are displayed in the numeric indicator labeled Count in the lower right quadrant of the front panel. The adjacent Reset button restores the count to zero.


Setup:

 Use the setup from either Part 2 or Part 5 of this Experiment.

Testing:

 Using an appropriate opaque object, block and unblock the beam. Verify that the count increases by one each time the object passes through the beam.

Observations:

 Examine the count VI. Write a brief summary of how it works.

Design Challenge:

 Create a Labview program that displays the total amount of time that the beam has been blocked. Include a button to reset the total. You can either create the program from scratch or start with the Binary program and add the additional functionality. If you do the latter, save a copy to your own directory before starting and work from that copy.