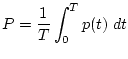 where
where The signal-to-noise ratio (SNR) is a measure of the quality of a signal received from a noisy system. As its name suggests, it is the ratio of the power of the desired signal to the power of the noise, usually expressed in decibels (dB).
In practice, it's not always easy to measure SNR. Although measuring the noise power in the absence of a signal is easy (just turn off the signal), if we could turn off the noise to make measurements, we'd just leave it off. In the lab is sometimes possible to turn off the noise or to estimate the uncorrupted signal amplitude. When we can't do this, we have to settle for what we can measure, usually noise alone and noise plus signal. This gives us the signal plus noise to noise ratio, or SNNR.
Whatever measurements we make, we need to express the
result as a ratio of powers.
At the frequencies we will be interested in, measuring
voltage is easier than measuring power.
If the signal of interest is connected to a resistor
of resistance ![]() , then by Joule's and Ohm's laws
the power delivered to the resistor is
, then by Joule's and Ohm's laws
the power delivered to the resistor is ![]() .
However, since the signal is a function of time,
so is the power:
.
However, since the signal is a function of time,
so is the power: ![]() .
If we want a single number to represent the power
of the signal, we can choose the
average power:
.
If we want a single number to represent the power
of the signal, we can choose the
average power:
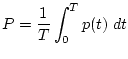 where
where ![]() is an interval of time sufficient to
contain the average behavior of the signal.
If
is an interval of time sufficient to
contain the average behavior of the signal.
If ![]() is periodic,
is periodic, ![]() is chosen to be an
integer multiple of the period.
is chosen to be an
integer multiple of the period.
Substituting our instantaneous power ![]() into the
above integral, we get:
into the
above integral, we get:
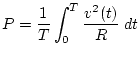 or
or
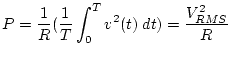 where
where
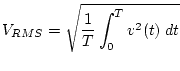 is called the
root mean square
or RMS
value of
is called the
root mean square
or RMS
value of ![]() .
.