
The Roots and Unwrapped Phase of Real Coefficient Polynomials
The Polynomial Club: C. Sidney Burrus, James Fox, Gary Sitton, and Sven Treitel 3/9/2006
Affiliate members: Joe Pat Lindsey and Ryan King
- Purpose
- Updates
- Installation
- What's New?
- The Lindsey-Fox Algorithm
- Sample executions
- Future changes
- Major functions
- Lesser functions
- Simplified version
- Comments
- John Mcnamee's bibliography of
polynomial factorization algorithmsPublications
Software
- Programs, Release 2 (as of April 2006)
ZIP file (size 4 MB)Example data (in Matlab *.mat format)
- The coefficients & roots of a 1 million degree polynomial.
ZIP file (size 14 MB)- An ill-conditioned 270 degree polynomial and its roots.
ZIP file (size 7 KB)- An ill-conditioned 200 degree polynomial and its roots.
ZIP file (size 5 KB)- A 1,000 degree sweep and its roots and unwrapped phase.
ZIP file (size 58 KB)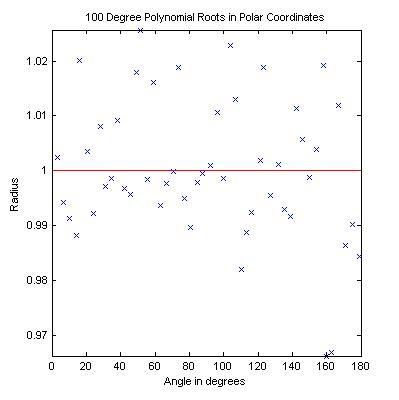
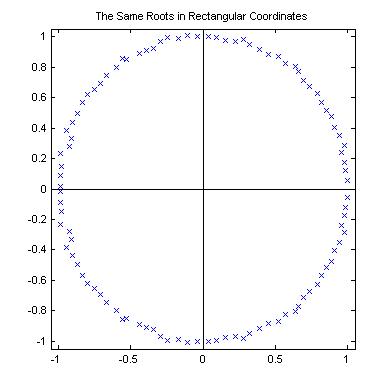
Three of the programs currently available on this site, lroots, broots, and unwrapz, are discussed in "Factoring Very High Degree Polynomials," IEEE Signal Processing Magazine, November 2003.
The first two programs are designed to factor the z-transforms of speech data, seismic data, and real random coefficient polynomials. These polynomials all have very similar root distributions. Furthermore, it is suspected that many polynomials whose coefficient sequence is not asymptotic to zero at either end will have similarly distributed roots. Therefore, although these programs may not work well for the general polynomial, they are likely to work for a large and important subclass of polynomials, especially those arising from signals.
Broots is a “find and deflate” algorithm that has been tried on 12 polynomials of degree 100,000. It successfully factored 9. However at degree 150,000 it successfully factored only 1 out of 5 polynomials.
Lroots is a “grid search” algorithm that has proven to be very successful by factoring hundreds of thousands of polynomials of degrees from one thousand to hundreds of thousand as well as 6 of degree one million, 4 of degree 2 million, and 1 of degree four million. The basic algorithm is parallel and is easily implemented on a parallel computer. The four million degree polynomial was factored on four processors of an AMD cluster running Linux. In April 2006 we replaced the 2004 version with Release 2 of the Lindsey-Fox Matlab programs on this site. The parallel version has not been released to the public yet.
Matlab's polynomial factorization function, roots, uses the eigenvalue method which generates the companion matrix of the given polynomial, and then finds the eigenvalues of that matrix. It is powerful, robust, and the preferred method for low and moderate degree polynomials. However, because of speed and memory requirements, it unsuitable for high degree polynomials.
Accurate phase unwrapping is acknowledged to be a difficult problem. However, Steiglitz and Dickinson observed that if one can accurately factor the z-transform, then one can accurately unwrap the phase. A Matlab program, unwrapz, to use the roots of a z-transform to unwrap its phase is included.
Two other phase unwrapping programs, unwrapm and unwraphp, take a different approach. Traditional phase uwrappers have problems if the phase jump is too large. However, this can be fixed. If the time series is doubled (or quadrupled, or more) in length by padding zeros, then the frequency interval is cut in half and the phase change from one sample to the next is decreased. If the phase change is decreased enough, then traditional phase unwrappers will work, or at least come very close.
More details can be found in the paper mentioned above. Our thanks to Ryan King, Anna Youssefi, and the Computer and Information Technology Institute (CITI) at Rice.
4/3/2006